Scilab #2 Metodo di Bisezione per determinare gli zeri di una funzione

Obiettivo: Determinare gli zeri di una funzione utilizzando il metodo di bisezione e sfruttando il software di calcolo numerico Scilab.

Il metodo di bisezione:

Il metodo di bisezione è un metodo numerico iterativo che serve per trovare una radice (zero) di una funzione continua su un intervallo [a, b], a condizione che la funzione cambi segno su quell’intervallo:

f(a)*f(b) < 0

Questo significa che la funzione passa da negativa a positiva (o viceversa), quindi c’è almeno uno zero in mezzo (per il teorema degli zeri di Bolzano).

Il funzionamento del metodo di bisezione:

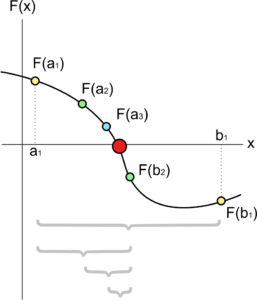
• Si sceglie un intervallo iniziale [a, b] tale che f(a)*f(b)<0
• Si calcola il punto medio c=(a+b):2
• Si valuta f(c):
• Se f(c)=0 si è trovata la soluzione esatta.
• Se f(a)*f(c)<0, la radice è tra a e c: si aggiorna il valore di b = c
• Se f(b)*f(c)<0, la radice è tra b e c: si aggiorna il valore di a = c
• Si ripete il procedimento fino a che l’intervallo è sufficientemente piccolo, cioè:∣b−a∣<tolleranza desiderata.

Codice:

Un esempio del metodo di bisezione viene effettuato utilizzando il seguente codice Scilab il quale ha l’obiettivo di determinare gli zeri della funzione:

y = cos(x) – x

Esercizi:

Graficare le seguenti funzioni utilizzando il software di calcolo numerico Scilab:

• y = x^3 nell’intervallo [-1, 1]
• y = x^3-x-2 nell’intervallo [1, 2]
• y = sin(x) – x/2 nell’intervallo [1, 2]