Obiettivo: Effettuare una semplice elaborazione di una immagine in scilab con l’obiettivo di aumentare o diminuire la luminosità di una foto.

Teoria Rappresentazione di una immagine:

Un’immagine in scala di grigi a 8 bit rappresenta ogni pixel con un singolo valore che descrive la sua luminosità. Questi valori possono variare da 0 (completamente nero) a 255 (completamente bianco), con 256 livelli intermedi che rappresentano diverse sfumature di grigio. Ogni pixel dell’immagine è associato a una matrice bidimensionale, dove ogni elemento della matrice contiene un valore di luminosità che definisce il tono di grigio di quel pixel. Nel contesto delle immagini a 8 bit, un’immagine in scala di grigi è generalmente memorizzata come una matrice di interi compresi tra 0 e 255. La rappresentazione in scala di grigi è particolarmente utile per applicazioni che richiedono analisi di luminosità o contrasto, come nel caso della visione artificiale, della fotografia in bianco e nero e nell’elaborazione delle immagini mediche.

Funzioni non lineari per modificare la luminosità:

Oltre alle funzioni iperboliche, altre funzioni non lineari come i logaritmi e le funzioni polinomiali sono utilizzate per modificare la luminosità dei pixel in modo non uniforme. Queste funzioni consentono di alterare l’intensità dei pixel in modo che alcune aree dell’immagine vengano più schiarite o scurite rispetto ad altre, permettendo così di applicare effetti visivi complessi.

Funzione Logaritmica:

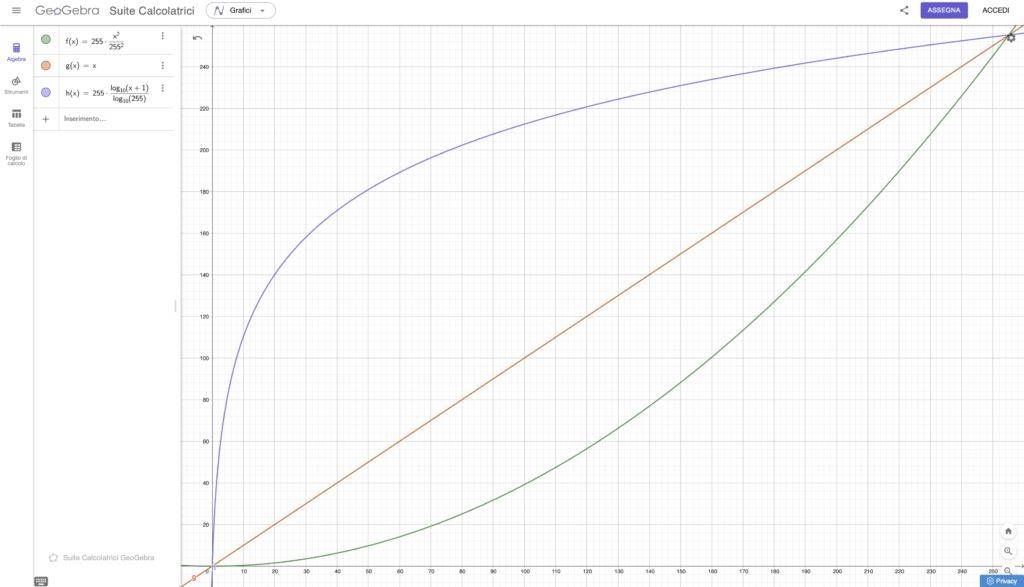
Una delle funzioni più comuni per manipolare la luminosità in modo non lineare è la funzione logaritmica. La funzione logaritmica è utile per schiarire le aree scure dell’immagine senza modificare troppo le aree già chiare. La formula logaritmica applicata ai valori dei pixel può essere espressa come:

h(x) = 255*log(x+1)/log(255)

Questa funzione ha l’effetto di aumentare la luminosità nelle aree scure dell’immagine, rendendo più visibili i dettagli nelle ombre. Tuttavia, non ha un impatto significativo sulle aree già luminose, poiché il logaritmo cresce più lentamente man mano che x x aumenta. È particolarmente utile quando si desidera “illuminare” le ombre senza sovraesporre le luci.

Funzione Polinomiale:

Le funzioni polinomiali sono un’altra classe di funzioni non lineari utilizzate per modificare la luminosità. Una funzione polinomiale di grado nn applicata ai valori dei pixel può essere scritta come:

f(x) = 255*x^2/255^2

Questa funzione ha l’effetto di diminuire la luminosità nelle aree chiare dell’immagine.

CONFRONTO TRA LE FUNZIONI:
Per comprendere al meglio l’effetto di queste funzioni sulle immagini vengono in seguito riproposti i differenti studi di funzione confrontati con l’equalizzazione della retta bisettrice del primo e del terzo quadrante

Codice SCILAB:
Il codice SCILAB presentato, si occupa di caricare un’immagine in formato .dat, applicare una trasformazione logaritmica per alterarne la luminosità e quindi visualizzare sia l’immagine originale che quella elaborata. Il codice è caratterizzato da differenti fasi:

• Lettura dell’immagine: Il codice legge un’immagine salvata in formato .dat (un formato di dati binari). La matrice che rappresenta l’immagine viene creata usando i valori di luminosità per ogni pixel. L’immagine è rappresentata come una matrice di dimensioni 1024×683.
• Elaborazione dell’immagine: Viene applicata una funzione logaritmica a ciascun pixel dell’immagine per modificarne la luminosità. La trasformazione logaritmica è progettata per schiarire le aree più scure dell’immagine, modificando l’intensità dei pixel.
• Visualizzazione delle immagini: Il codice mostra due versioni dell’immagine:

  • La versione originale, letta dal file .dat.
  • La versione elaborata, che ha subito la trasformazione logaritmica per modificare la luminosità.

In sostanza, l’immagine viene letta e poi trasformata utilizzando una formula logaritmica per migliorare la visibilità delle aree scure, per poi visualizzare entrambe le immagini.

FILE immagine:

https://www.arduinofacile.it/wp-content/uploads/2025/02/immagine.dat_.zip

Obiettivo: Determinare gli zeri di una funzione utilizzando il metodo di bisezione e sfruttando il software di calcolo numerico Scilab.

Il metodo di bisezione:

Il metodo di bisezione è un metodo numerico iterativo che serve per trovare una radice (zero) di una funzione continua su un intervallo [a, b], a condizione che la funzione cambi segno su quell’intervallo:

f(a)*f(b) < 0

Questo significa che la funzione passa da negativa a positiva (o viceversa), quindi c’è almeno uno zero in mezzo (per il teorema degli zeri di Bolzano).

Il funzionamento del metodo di bisezione:

• Si sceglie un intervallo iniziale [a, b] tale che f(a)*f(b)<0
• Si calcola il punto medio c=(a+b):2
• Si valuta f(c):
• Se f(c)=0 si è trovata la soluzione esatta.
• Se f(a)*f(c)<0, la radice è tra a e c: si aggiorna il valore di b = c
• Se f(b)*f(c)<0, la radice è tra b e c: si aggiorna il valore di a = c
• Si ripete il procedimento fino a che l’intervallo è sufficientemente piccolo, cioè:∣b−a∣<tolleranza desiderata.

Codice:

Un esempio del metodo di bisezione viene effettuato utilizzando il seguente codice Scilab il quale ha l’obiettivo di determinare gli zeri della funzione:

y = cos(x) – x

Esercizi:

Graficare le seguenti funzioni utilizzando il software di calcolo numerico Scilab:

• y = x^3 nell’intervallo [-1, 1]
• y = x^3-x-2 nell’intervallo [1, 2]
• y = sin(x) – x/2 nell’intervallo [1, 2]

Obiettivo: Analizzare alcune semplici funzioni elementari utilizzando il software di calcolo numerico Scilab.

Principi di calcolo numerico

Quando a scuola si studiano funzioni come sin(x), cos(x), 3x, etc… si pensa alle funzione come ad un oggetto continuo.
Nel immaginario comune, esistono un’infinità di valori tra due numeri, mentalmente è possibile “zoomare” in modo arbitrario la funzione, e questa avrà sempre un valore.
E’ importante considerare che un software di calcolo numerico come Scilab non può fare questo.
Nel dettaglio, Scilab, invece di “conoscere” tutta la curva, fa una cosa molto più semplice e concreta:

• Crea un vettore di punti del dominio (es. da 0 a 2π , con passo 0.1)
• Valuta la funzione solo per quei punti
• Memorizza in un vettore i punti del codominio
• Collega i punti con seguenti sul grafico.

Nel codice presentemente riportato il software di calcolo numeri ha:

• Ha preso circa 63 valori di x (da 0 a 2π)
• Per ognuno ha calcolato sin⁡(x)
• Ha ottenuto una lista di coppie (x, y)
• Ha disegnato il grafico unendo i punti con delle linee

Un secondo metodo utile per graficare le funzioni, sicuramente meno intuitivo, è quello di utilizzare un ciclo for per elaborare un punto alla volta. Dal punto di vista pratico questo approccio è sicuramente molto meno intuitivo d’altro canto è sicuramente utile per rendere visibile cosa fa Scilab internamente, cioè valutare la funzione punto per punto.

Esercizi:

Graficare le seguenti funzioni utilizzando il software di calcolo numerico Scilab:

• y = x^2
• y = 10cos(x)
• y = sin(10*x)
• y = x^2+4*x+6