ARDWARE #15 Sintesi di Circuiti Logici – Prodotto di Somme
Obiettivo: Imparare a sintetizzare il comportamento di un circuito combinatorio partendo da una specifica tabella di verità mediante il prodotto di somme.
Componenti elettronici:
- Porte Logiche (i.e., AND, OR, e NOT)
Teoria: Un circuito combinatorio è costituito da una serie di porte logiche opportunamente collegate tra loro con l’obiettivo di implementare una specifica funzione logica. Alcune delle porte logiche più utilizzate nell’ingegneria dell’informazione sono le porte: AND OR e NOT.
Le principali operazioni associate ad una rete logica sono due:
- Analisi di una rete logica: dato un circuito combinatorio vengono determinate la funzione logica e la tabella di verità.
- Sintesi di una rete logica: data la tabella di verità viene determinato il circuito combinatorio che implementa la rete.
Nel corso di questa lezione l’attenzione sarà focalizzata sulla sintesi di una rete logica. Nello specifico, la tecnica presentata per effettuare la sintesi di una rete logica viene denominata Prodotto di Somme e consiste in una procedura algoritmica che può essere facilmente applicata a tutte le differenti tabelle di verità.
Un’altra tecnica utilizzata per la sintesi di una rete logica è la somma di prodotti. Maggiori dettagli sono forniti al seguente link:
Il PRODOTTO DI SOMME (PoS – Product of Sum) è costituito dal prodotto logico dei maxtermini associati alle righe della tabella nella quale l’uscita assume valore 0.
Nel dettaglio un maxtermine è definito come la somma logica delle variabili booleane prese in forma diretta o negata a seconda se assumono valore 0 o 1.
A seguire, viene riportata la tabella dei maxtermini.
| A | B | C | Maxtermine |
| 0 | 0 | 0 | A+B+C |
| 0 | 0 | 1 | A+B+C |
| 0 | 1 | 0 | A+B+C |
| 0 | 1 | 1 | A+B+C |
| 1 | 0 | 0 | A+B+C |
| 1 | 0 | 1 | A+B+C |
| 1 | 1 | 0 | A+B+C |
| 1 | 1 | 1 | A+B+C |
In analogia alla tabella di verità, è importante considerare che date n variabili di input il numeri di maxtermini è pari a 2n.
Esempio:
Al fine di illustrare in dettaglio il processo di prodotto di somme viene riportato un esempio specifico partendo dalla seguente tabella di verità:
| A | B | C | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
1) Si prendono in considerazione solamente le uscite pari a 0 della tabella di verità, per ogni uscita si prendono i maxtermini di riferimento.
Input: 1 0 0 -> Maxtermine: A+B+C
Input: 1 1 1 -> Maxtermine: A+B+C
2) Si moltiplicano le somme precedentemente determinate per ottenere la funzione logica che implementa la tabella di verità di partenza.
Y= (A+B+C)*(A+B+C)
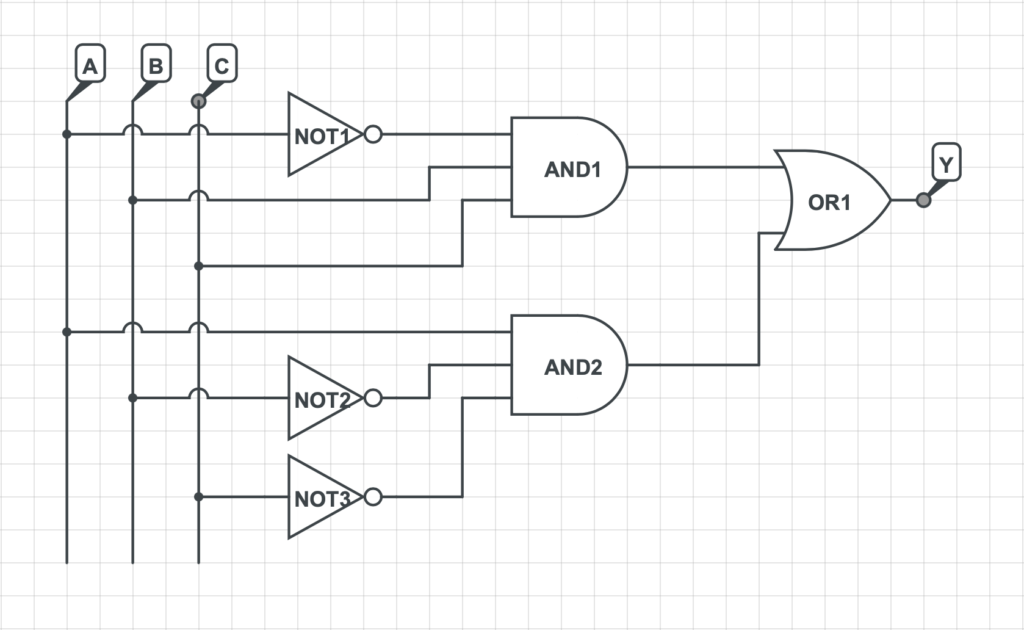
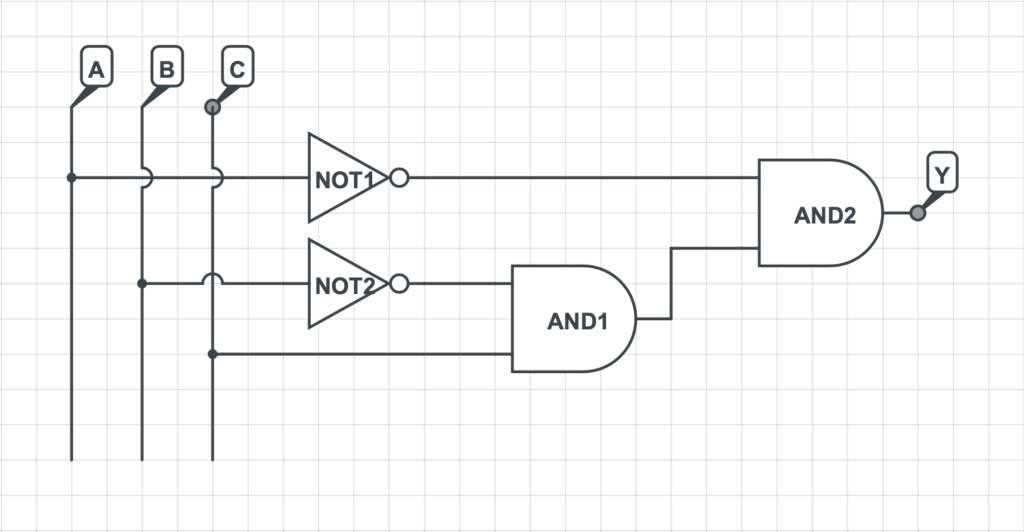
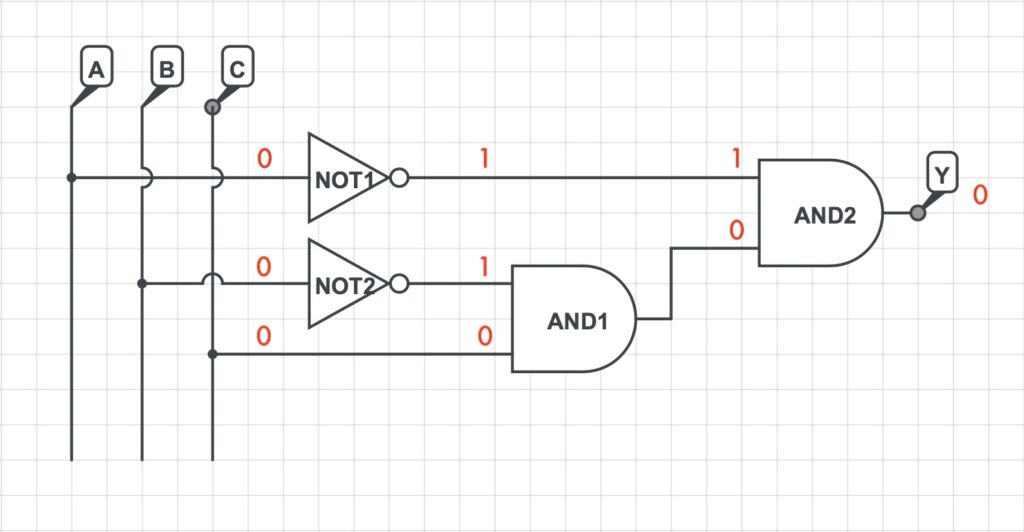
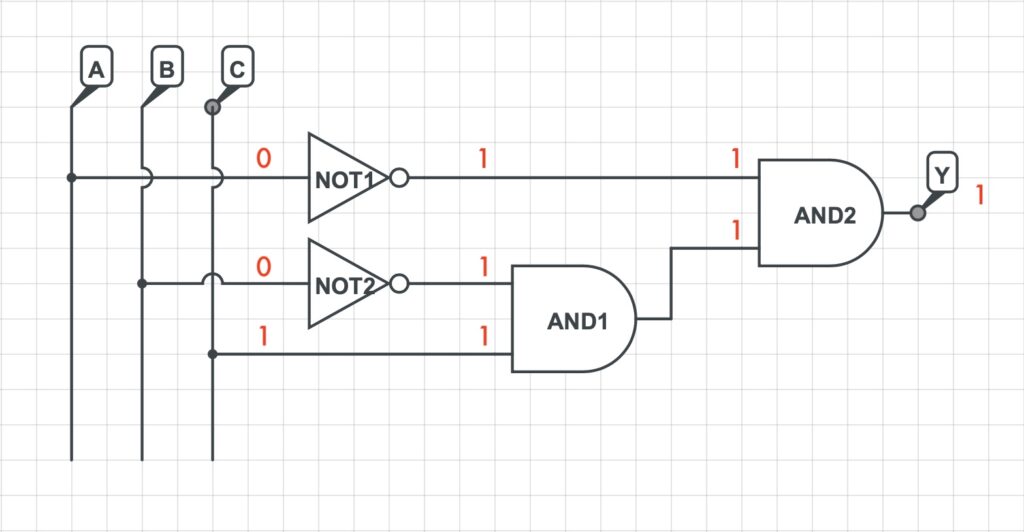
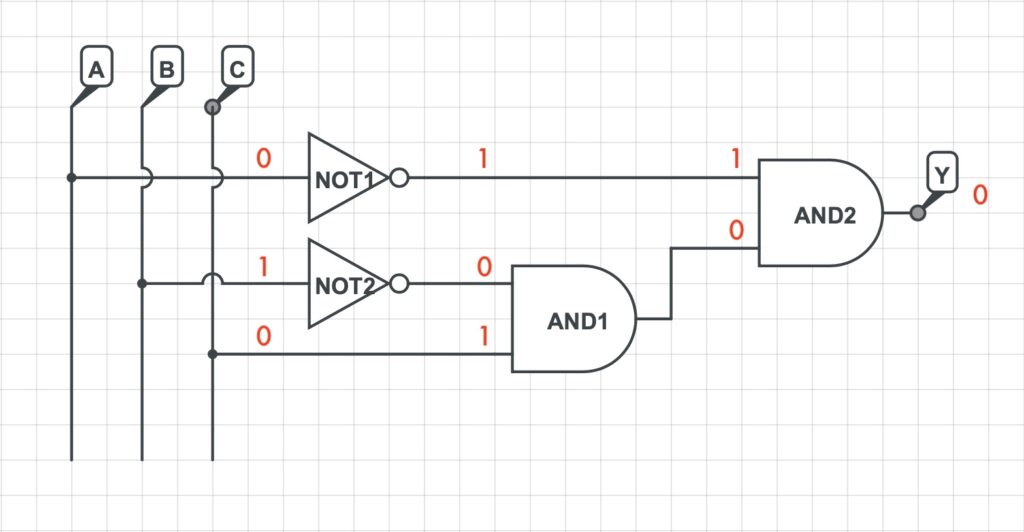
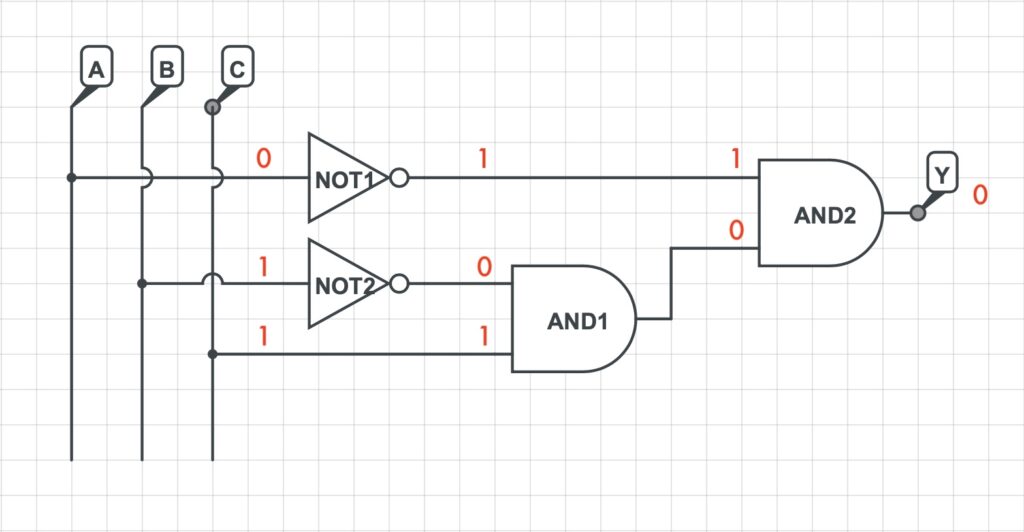
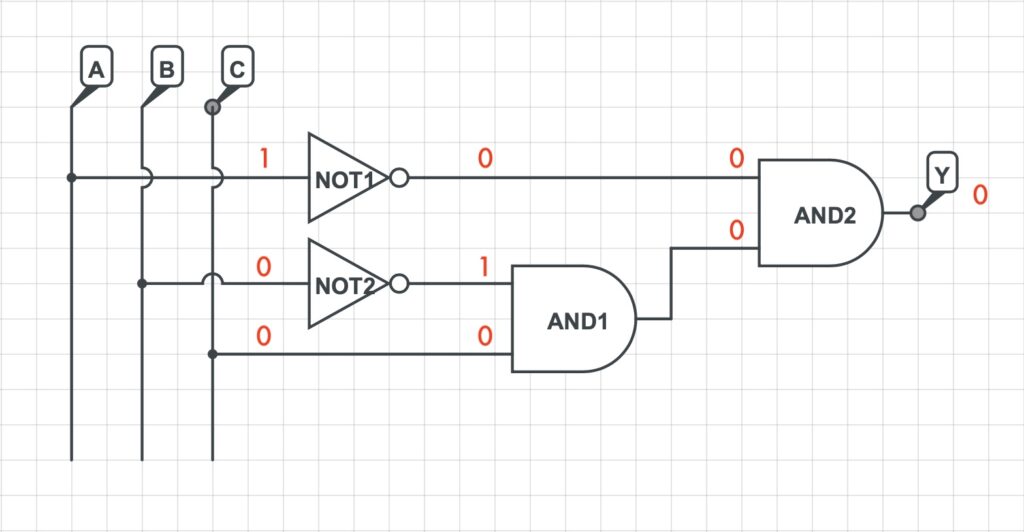
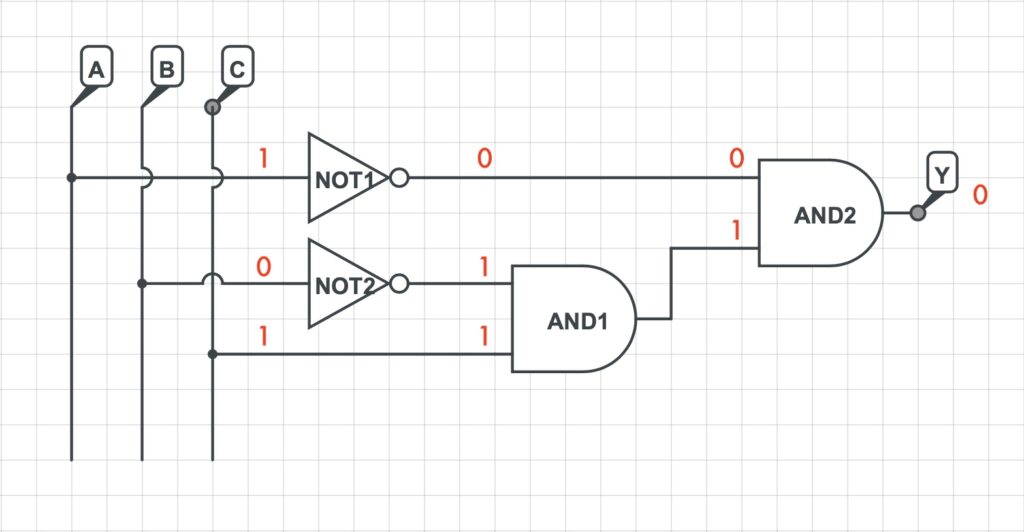
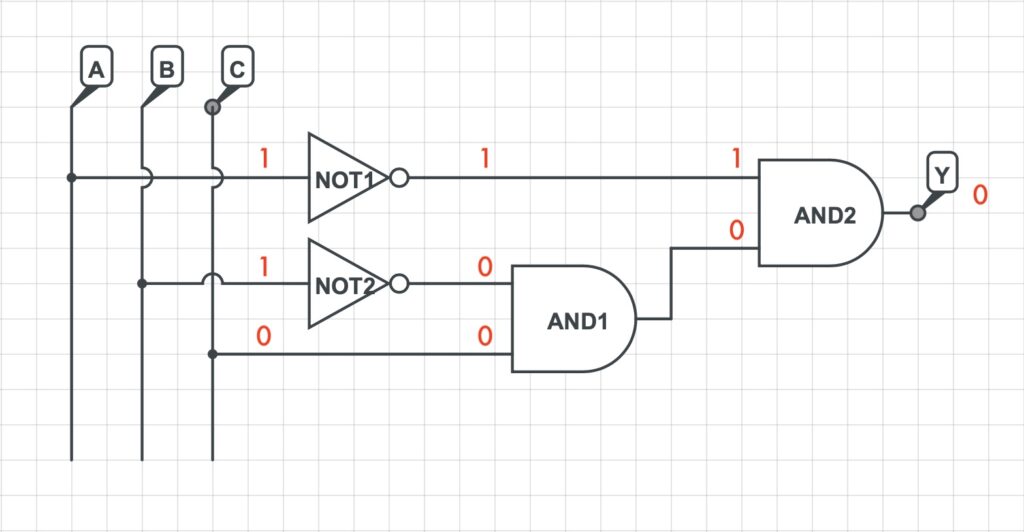
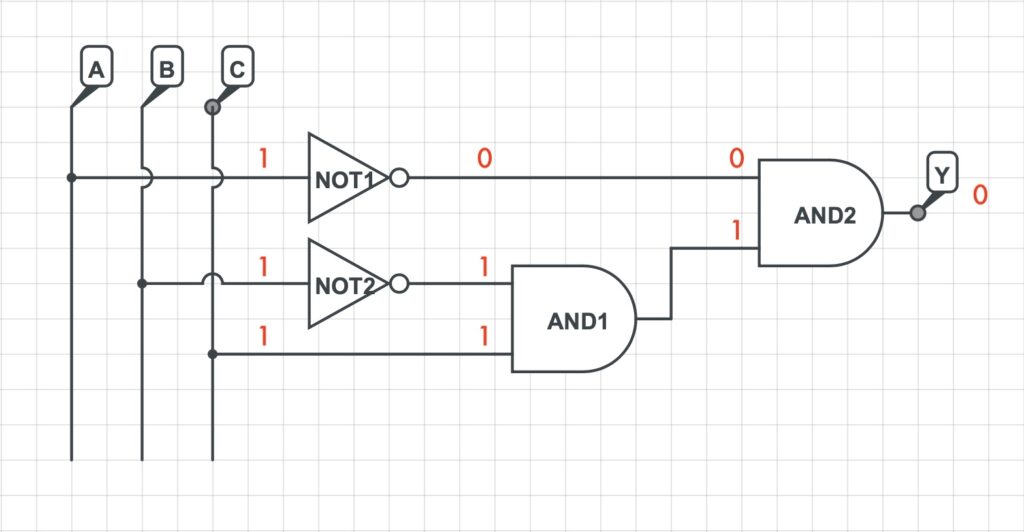
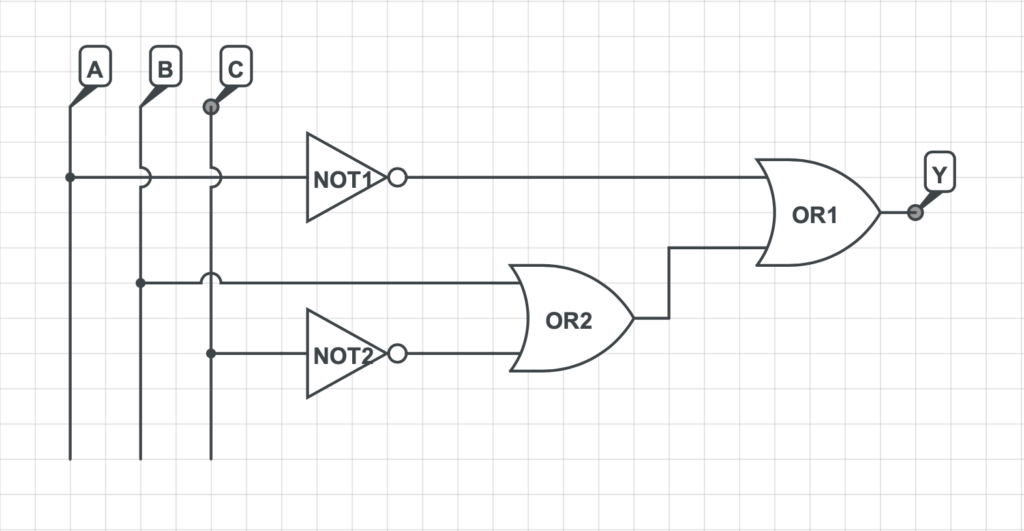
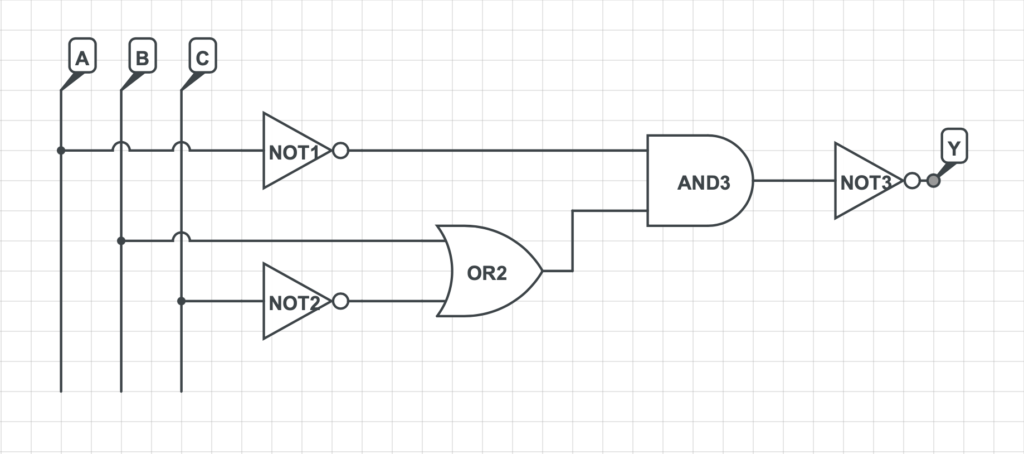
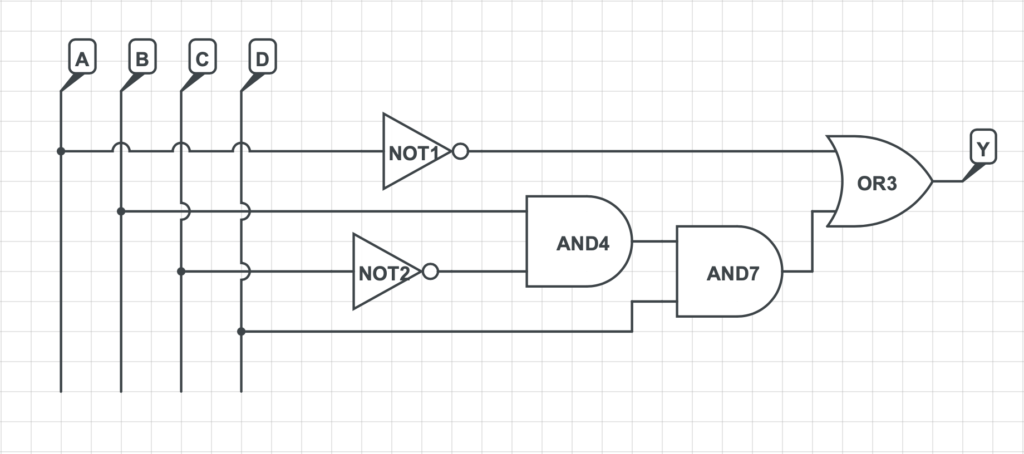
3) Si rappresenta la rete logica che implementa la funzione logica precedentemente determinata.
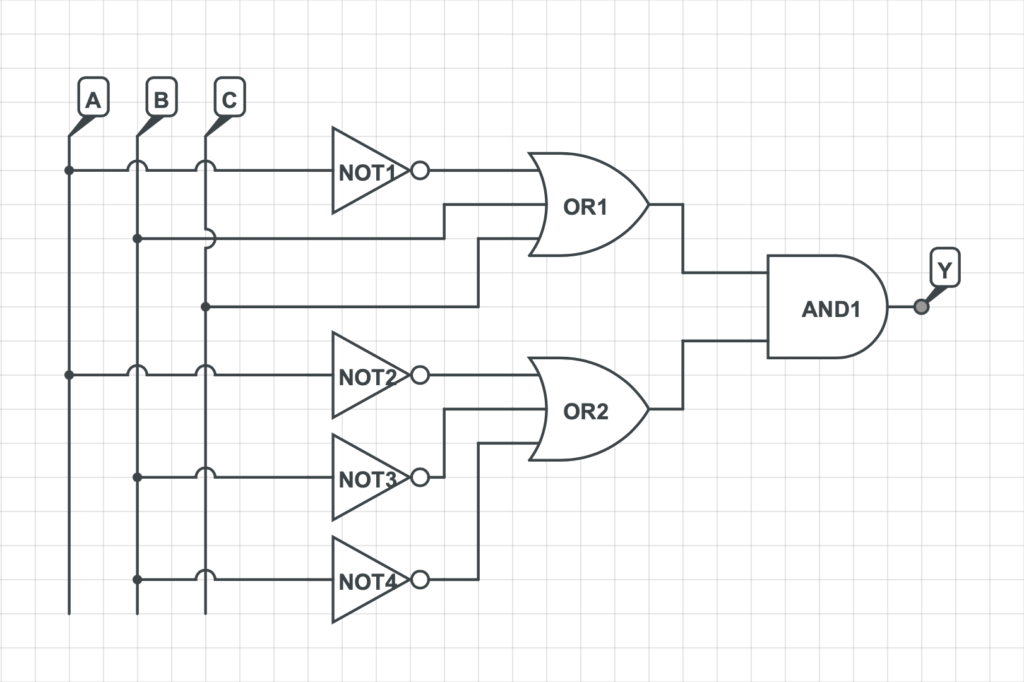
Esercizi di Approfondimento:
Vengono in seguito riportati alcuni esercizi che possono essere facilmente eseguiti al fine di comprendere se i concetti presentati sono stati opportunamente acquisiti. Pertanto si chiede di determinare la rete combinatoria legata alle seguenti tabelle di verità:
- Esercizio 1
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
- Esercizio 2
| A | B | C | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Considerazioni:
Le principali tecniche utilizzate per la sintesi di una rete logica, sono la somma di prodotti (SoP) ed il prodotto di somme (PoS). Sebbene il procedimento applicato possa sembrare analogo e pertanto la scelta del metodo di sintesi possa risultare ad appannaggio del progettista, in realtà i due metodi presentano differenti vantaggi computazionali in base alla tabella di verità da sintetizzare.
Nello specifico per tabelle di verità la cui uscita assume più facilmente un valore pari ad 1 è opportuno utilizzare la somma di prodotti.
Differentemente per tabelle di verità la cui uscita assume più facilmente un valore pari ad 0 è opportuno utilizzare il prodotto di somme.