ARDWARE #12 Analisi di Circuiti Logici – Circuito Combinatorio
Obiettivo: Imparare ad analizzare il comportamento di un circuito combinatorio costituito dalla connessione di più porte logiche.
Componenti elettronici:
- Porte Logiche (i.e., AND, OR, e NOT)
Teoria: Un circuito combinatorio è costituito da una serie di porte logiche opportunamente collegate tra loro con l’obiettivo di implementare una specifica funzione logica.
E’ importante considerare che le reti logiche combinatorie sono quelle reti in cui lo stato d’uscita dipende solamente dal valore degli ingressi assunto in quel determinato istante.
Al fine di poter analizzare un circuito combinatorio è opportuno conoscere il funzionamento delle singole porte logiche che costituiscono il circuito stesso.
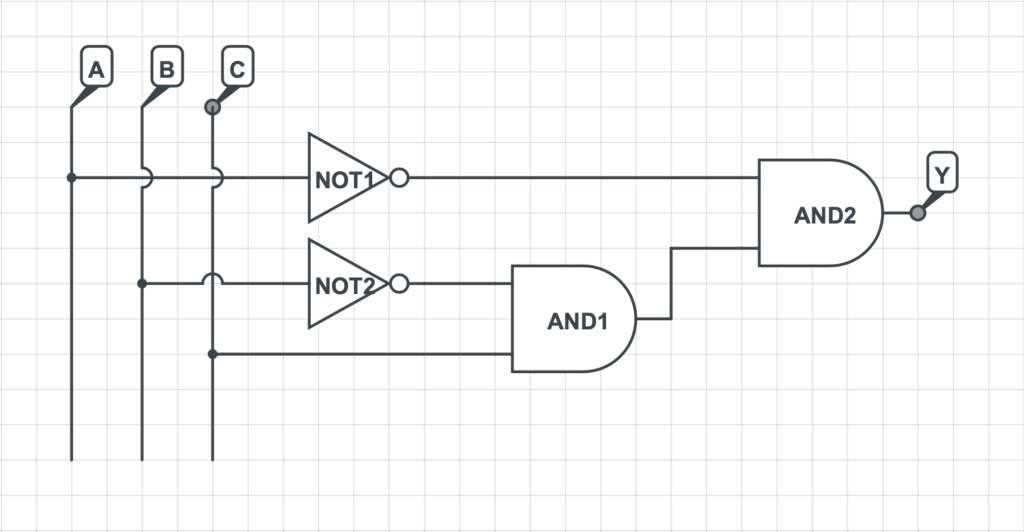
Viene in seguito riportato un esempio di circuito combinatorio. Tale circuito sarà analizzato considerando tutte le possibili combinazioni di valori assunti dai differenti input del sistema con l’obiettivo di determinarne la tabella di verità della rete logica combinatoria.
Nello specifico il circuito presenta tre differenti ingressi: l’ingresso A, l’ingresso B e l’ingresso C. Pertanto le possibili combinazioni di valore assunte dai vari input del sistema sono 8 (2 elevato alla terza).
Viene in seguito riportata la tabella di verità con tutte le possibili combinazioni di valori assunte dall’ingresso. Compito dell’operazione di analisi è determinare il valore Y assunto per ogni specifico valore dell’ingresso.
| A | B | C | Y |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
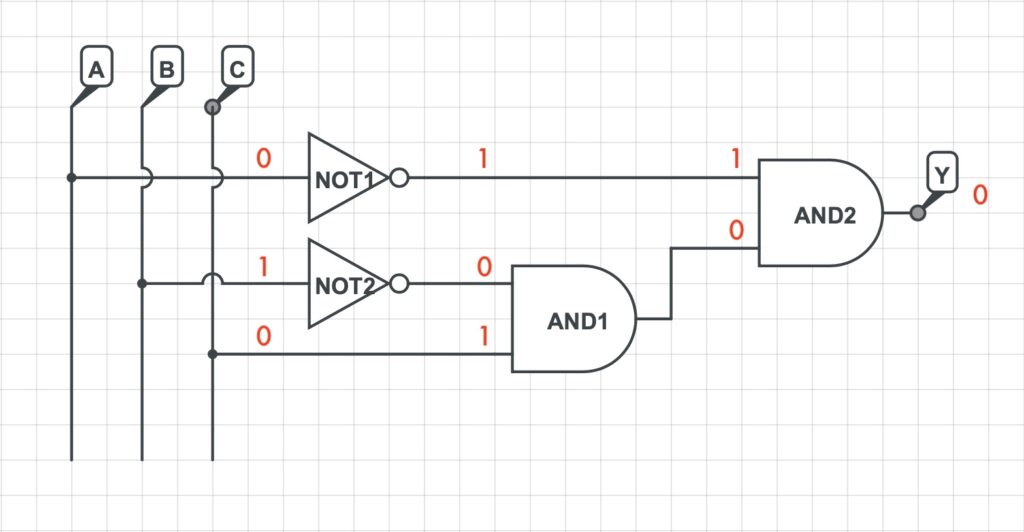
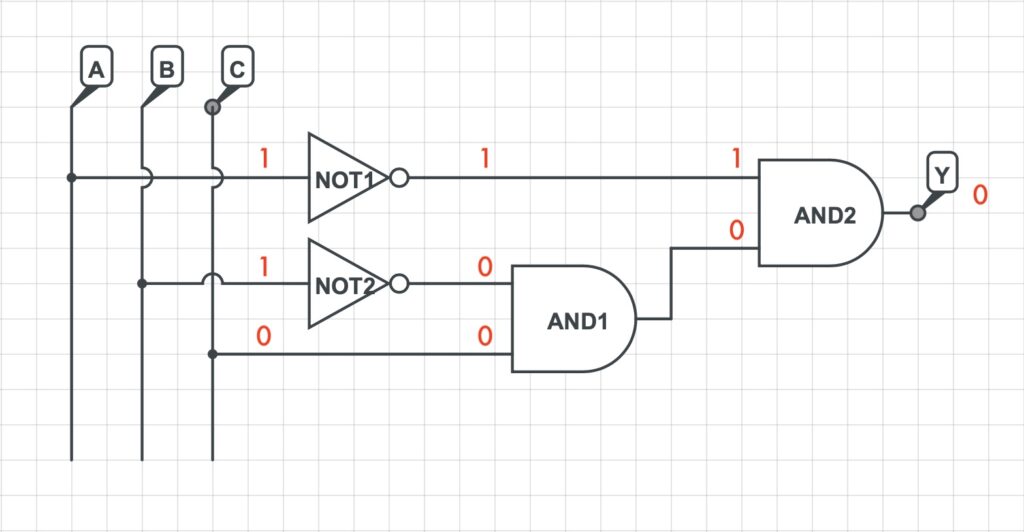
Come primo esempio sarà determinato il valore dell’uscita y quando A = 0, B = 0 e C = 0.
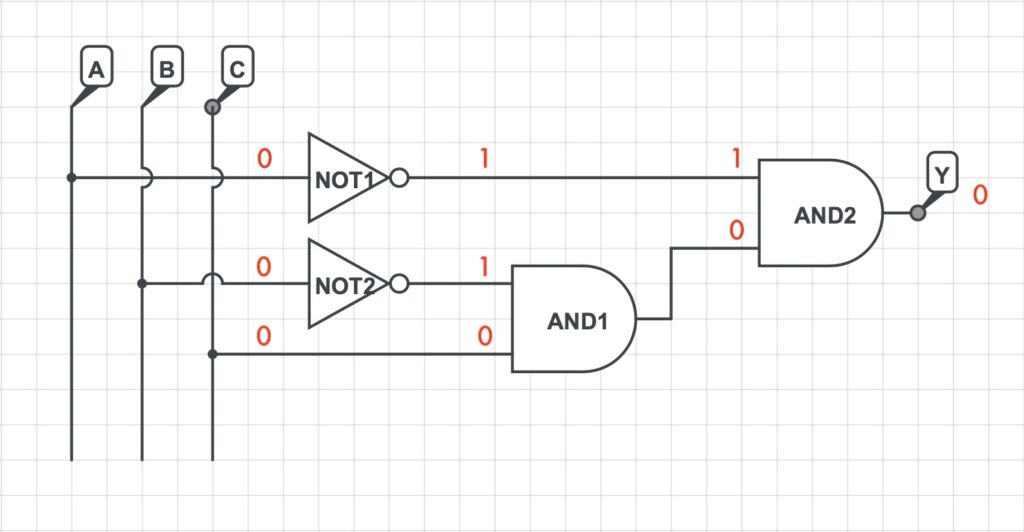
Poichè l’ingresso della porta logica NOT1 risulta essere uguale a 0 il suo valore in uscita sarà pari ad 1. Le stesse considerazioni valgono per la porta logica NOT2. Considerando inoltre la tabella di verità della porta logica AND, l’uscita della porta logica AND1 risulterà essere uguale a 0 e di conseguenza anche l’uscita della porta logica AND2. In conclusione si può facilmente affermare che per l’ingresso A = 0, B = 0, C = 0, il valore dell’uscita Y è pari a 0.
Si analizzerà in seguito il valore dell’uscita per tutte le possibili combinazioni.
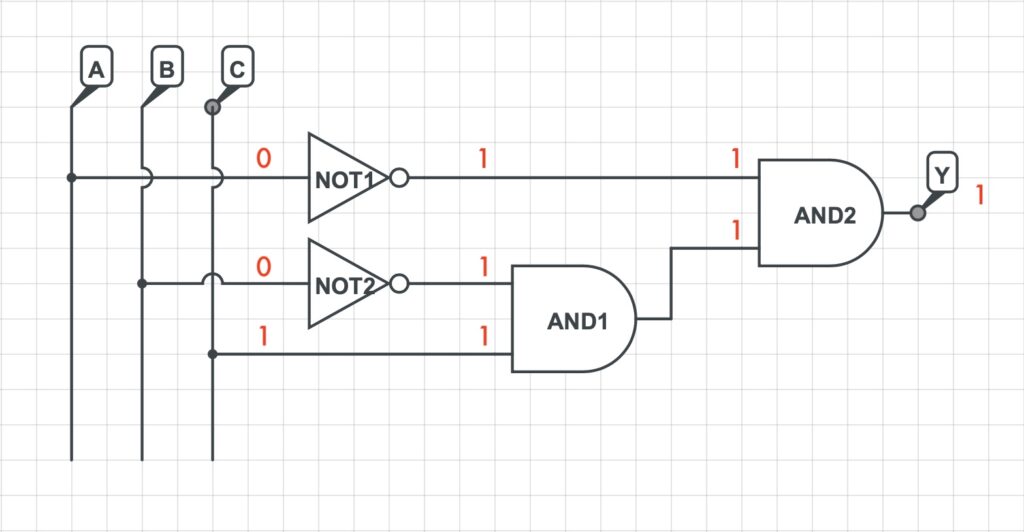
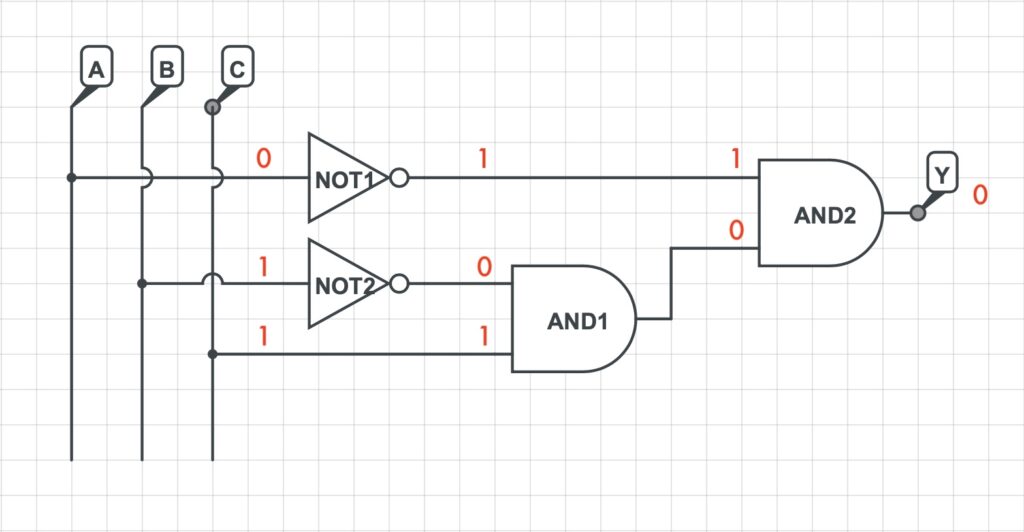
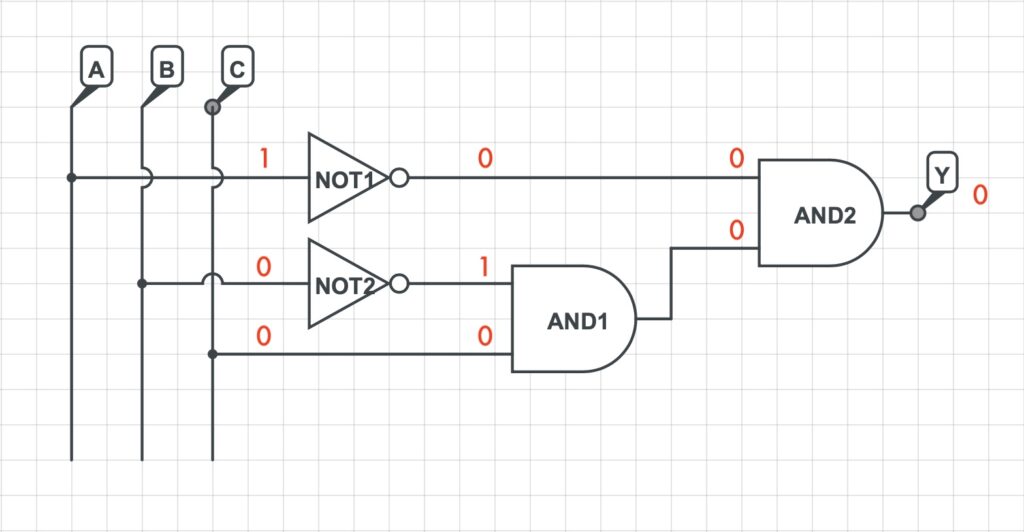
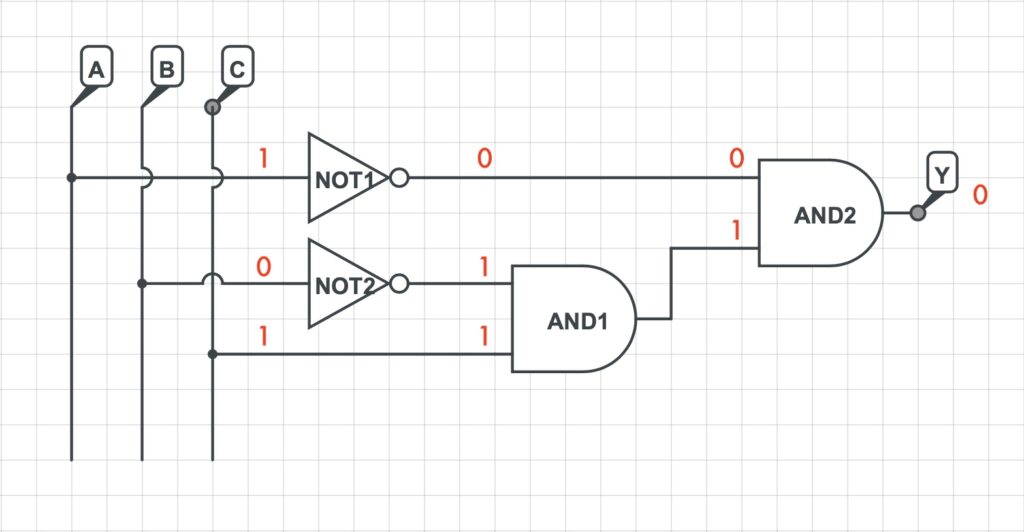
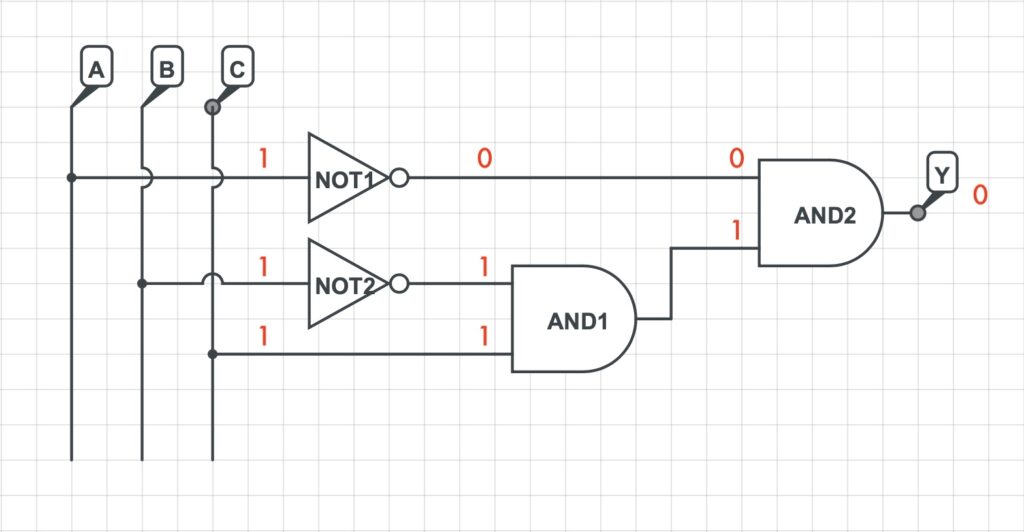
Pertanto, dalla precedente analisi è facilmente determinabile la tabella di verità della suddetta rete logica
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Esercizi di Approfondimento
Vengono in seguito riportati alcuni esercizi che possono essere facilmente eseguiti al fine di comprendere se i concetti presentati sono stati opportunamente acquisiti. Pertanto si chiede di determinare le tabelle di verità delle seguenti reti combinatorie.
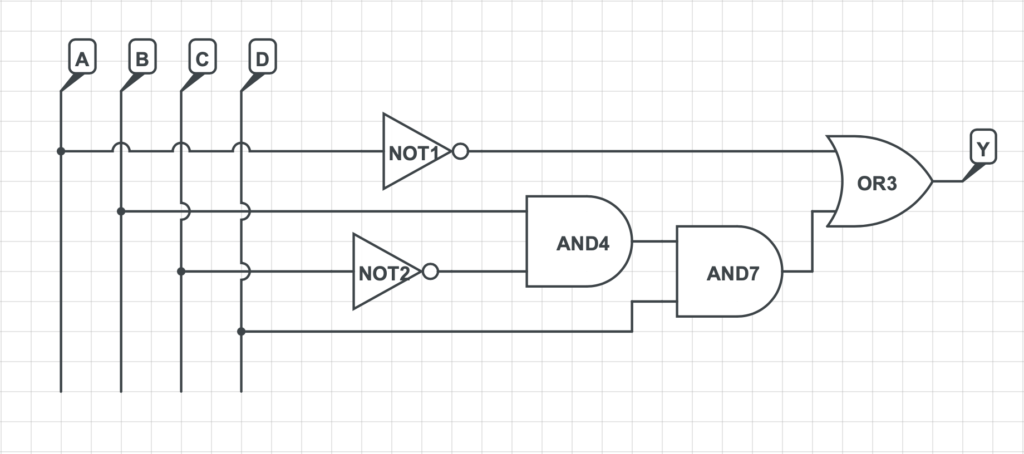
- Esercizio 1
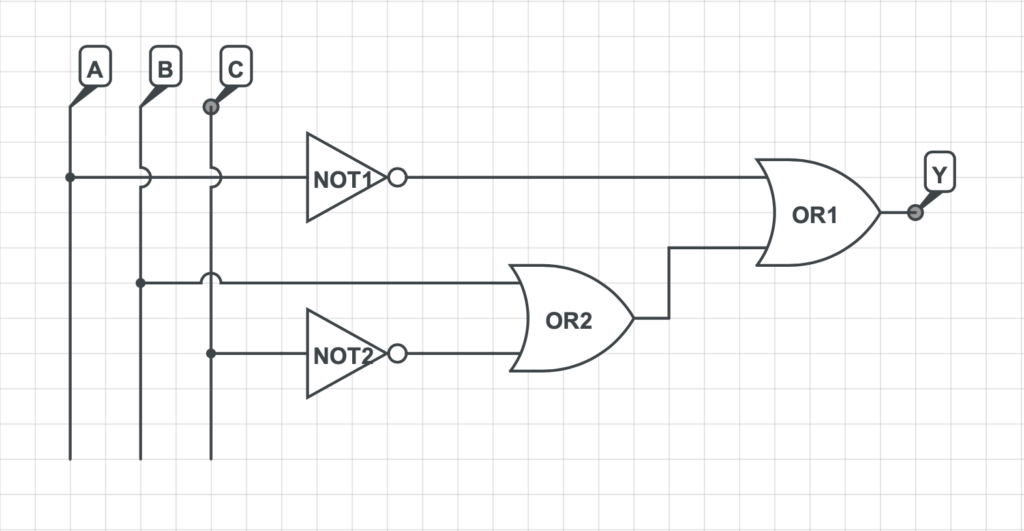
- Esercizio 2
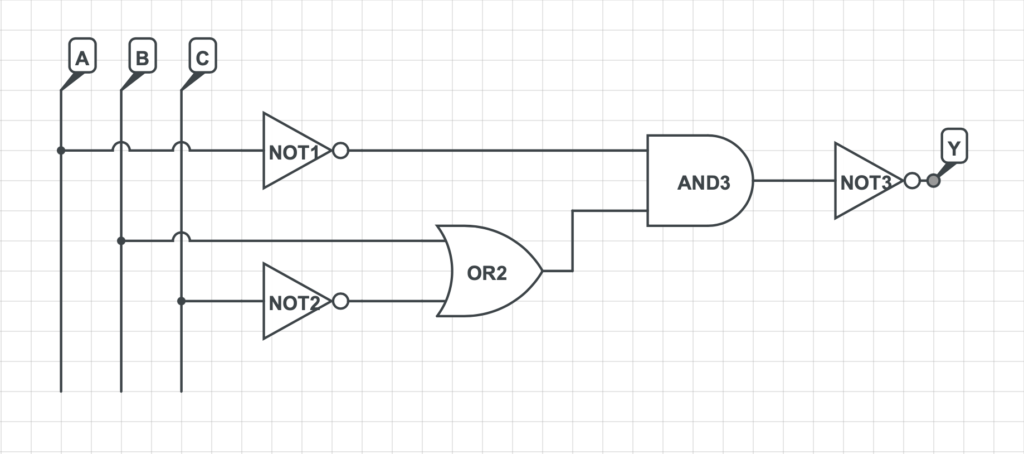
- Esercizio 3